SEE Optional Mathematics Model Question 2080

SEE Optional Mathematics New Specification Grid 2080

MODEL QUESTION 2080

Subject: Optional Mathematics

Class: 10

Full Marks: 75

Time: 3 hrs

All the questions are compulsory.

Note: Due to limitation of blogger, I was unable to use the vector symbol on question no. 9, 17 and 32. So, add vector symbols accordingly while you practice this set.

Group A [10 × 1 = 10]

Define trigonometric function.
✎ Trigonometric function is the function of an angle expressed as the ratio of two sides of a right-angled triangle. The most common trigonometric functions are sine, cosine, and tangent.

For example:

sin θ = P/h, cos θ = b/h, and tan θ = P/b
What is arithmetic mean between two numbers a and b?
✎ The arithmetic mean (AM) between two numbers a and b is:

AM = (a + b) / 2
Write the name of the set of numbers which is continuous.
✎ The set of real numbers is continuous.
If matrix A = [[a, b], [c, d]], what is the value of |A|?
✎ The value of |A| is:

|A| = ad - bc
If the angle between two straight lines is θ and their slopes are m₁ and m₂ respectively, write the formula for tan θ.
✎ Here, the formula for tan θ is:

tan θ = ±(m₁ - m₂) / (1 + m₁m₂)
Which geometric figure will be formed if a plane intersects a cone parallel to its base?
✎ A circle will be formed if a plane intersects a cone parallel to its base.
Express sin 2A in terms of tan A.
✎ sin 2A can be expressed in terms of tan A as:

sin 2A = (2 tan A) / (1 + tan² A)

Define angle of elevation.
✎ The angle of elevation is the angle between a horizontal line from the observer and the line of sight to an object that is above the horizontal line.
What is the scalar product of two vectors a and b if the angle between them is θ?
✎ Here, the scalar product of given vectors is:

a · b = |a||b|cosθ
If P' is image of P and r is radius of inversion circle with center O in an inversion transformation, write the relations of OP, OP', and r.
✎ The relations of OP, OP', and r is:

OP × OP' = r²

Group ‘B’ [8 × 2 = 16]

If 2x³ − 7x² + x + 10 = (x − 1)Q(x) + R, find the remainder R and quotient Q(x).
✎ Here, 2x³ − 7x² + x + 10 = (x − 1)Q(x) + R

Comparing (x − 1) with (x − a), we get a = 1.

Now, using Synthetic Division:
```
            
x³   x²   x     x°
2   −7    1    10
↓    2   −5    −4    
2   −5   −4     6 = R
x²   x    x°

            
```
Now,

Quotient = Q(x) = 2x² − 5x − 4

Remainder = R = 6
Write down the inequality represented by the shaded region in the adjoining figure.
✎ From the given figure, the boundary line passes through the points (4, 0) and (0, −3). So, the equation of boundary line is:

y − y₁ = (y₂ − y₁) / (x₂ − x₁) (x − x₁)

or, y − 0 = (−3 − 0) / (0 − 4) (x − 4)

or, y = (3/4)(x − 4)

or, 4y = 3x − 12

∴ 3x − 4y = 12

Since, the half plane with the boundary line contains origin, so the inequality represented by the shaded region is:

3x − 4y ≤ 12

Find the determinants D and D₂ of coefficients of x and y by using Cramer's rule from the equations 4x − 5y = 2 and 3x + 4y = 48.

✎ Here,

4x − 5y = 2 ...(i)

3x + 4y = 48 ...(ii)

Now, arranging the coefficients and constant term, we get:

Coeff. of x	Coeff. of y	Constant
4	-5	2
3	4	48

Now,

| 2 -5 |

| 48 4 |

= 2×4 − 48×(−5) = 8 + 240 = 248

D₂:

| 4 2 |

| 3 48 |

= 4×48 − 3×2 = 192 − 6 = 186

Find the slopes of two straight lines 3x + 4y = 5 and 6x + 8y + 7 = 0 and write the relationship between them.
✎ Slope of 3x + 4y = 5 is m₁ = -coeff. of x / coeff. of y = -3 / 4

Slope of 6x + 8y + 7 = 0 is m₂ = -coeff. of x / coeff. of y = -6 / 8 = -3 / 4

Since m₁ = m₂, the given lines are parallel.
Convert sin6A.cos4A into sum or difference of sine or cosine.
✎ We know that, 2sinAcosB = sin(A+B) + sin(A−B)

Now,

sin6Acos4A = (1/2) × 2sin6Acos4A

= (1/2)[sin(6A + 4A) + sin(6A − 4A)]

= (1/2)[sin10A + sin2A]
If 2sinθ = √3, find the value of θ. (0° ≤ θ ≤ 180°)
✎ Here,

2sinθ = √3

or, sinθ = √3 / 2

or, sinθ = sin60°

∴ θ = 60°

Again,

sinθ = sin60° = sin(180° − 60°) = sin120°

∴ θ = 120°

Thus, the values of θ are 60° and 120°.
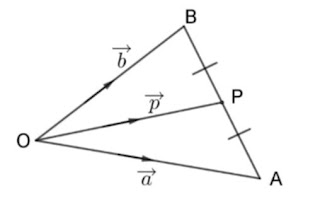
O is the origin in the given figure. If a and b are the position vectors of the points A and B, show that the position vector of the point P is p = 1/2 (a + b).

✎ Here,

OA = a
,
OB = b
, and
OP = p

Now,

AP = PB

or,

AO + OP = PO + OB

or,

-OA + OP = -OP + OB

or,

-a + p = p + b

or,

p + p = a + b

or,

2p = a + b

or,

p = (a + b)/2

∴
p = (a + b)/2
In a series, the first quartile (Q₁) = 35 and third quartile (Q₃) = 75, find the quartile deviation and its coefficient.
✎ Here, Q₁ = 35 and Q₃ = 75
Now,
Quartile Deviation (QD) = (Q₃ - Q₁) / 2
= (75 - 35) / 2
= 40 / 2
= 20

Coefficient of Quartile Deviation = (Q₃ - Q₁) / (Q₃ + Q₁)
= (75 - 35) / (75 + 35)
= 40 / 110
= 0.36

Group ‘C’ [11 × 3 = 33]
If two functions are f(x) = (2x + 5) / 8 and g(x) = 3x - 4, find (f ∘ g)^-1(3).
✎ Here, f(x) = (2x + 5) / 8 and g(x) = 3x - 4
Now,
f ∘ g(x) = f(g(x))
= f(3x - 4)
= [2(3x - 4) + 5] / 8
= (6x - 8 + 5) / 8
= (6x - 3) / 8
Let f ∘ g(x) = (6x - 3) / 8 = y

To find (f ∘ g)^-1(x), interchanging the roles of x and y and solving for y,
6y - 3 / 8 = x
or, 6y - 3 = 8x
or, y = 8x + 3 / 6
or, (f ∘ g)^-1(x) = 8x + 3 / 6
So, (f ∘ g)^-1(3) = 8 x 3 + 3 / 6 = 9 / 2

Solve by graphical method: 2x² + x - 6 = 0

✎ Here, 2x² + x - 6 = 0
or, 2x² = 6 - x
Let y = 2x² = 6 - x
Then, y = 2x² ... (i)
y = 6 - x ... (ii)

Equation (i) represents the parabola with vertex at origin and equation (ii) represents a straight line. The point of intersection of the parabola and straight line gives the solution.

From equation (i), y = 2x²

x	-2	-1	0	1	2
y	8	2	0	2	8

Plotting these points on the graph and joining them, we get a parabola with vertex at origin.

From equation (ii), y = 6 - x

x	0	2
y	6	4

Plotting these points on the graph and joining them, we get a straight line.

From the graph, the points of intersection of the parabola and straight line are (-2, 8) and (1.5, 4.5).
∴ x = -2, 1.5

For a real valued function f(x) = 2x + 3, find the values of f(2.99), f(3.01), and f(3). Is this function continuous at x = 3?
✎ Here, f(x) = 2x + 3
Now,
f(2.99) = 2 × 2.99 + 3 = 8.98
f(3.01) = 2 × 3.01 + 3 = 9.02
f(3) = 2 × 3 + 3 = 9

When x = 2.99 → 3⁻, f(x) = 8.98 → 9
∴ lim_x→3⁻ f(x) = 9
When x = 3.01 → 3⁺, f(x) = 9.02 → 9
∴ lim_x→3⁺ f(x) = 9
When x = 3, f(3) = 9
∴ lim_x→3⁻ f(x) = lim_x→3⁺ f(x) = f(3) = 9
Thus, function f(x) is continuous at x = 3.
By using the matrix method solve the following systems of equations:
3x + 5y = 11, 2x - 3y = 1

✎ Here,
3x + 5y = 11
2x - 3y = 1

Writing in matrix form, x
Find the equations of pair of lines represented by equation 6x² - xy - y² = 0 and also find the angle between them.
✎ Here,
6x² - xy - y² = 0
or, 6x² - (3 - 2)xy - y² = 0
or, 6x² - 3xy + 2xy - y² = 0
or, 3x(2x - y) + y(2x - y) = 0
or, (2x - y)(3x + y) = 0

Thus, the two separate equations are: 2x - y = 0 and 3x + y = 0

Comparing 6x² - xy - y² = 0 with ax² + 2hxy + by² = 0, we get:

a = 6, 2h = -1 → h = -1/2 and b = -1

Now, The angle between the pair of lines is given by:

tan θ = ± 2√(h² - ab) / (a + b)

Substituting values:

tan θ = ± 2√((-1/2)² - 6(-1)) / (6 - 1)
= ± 2√(1/4 + 6) / 5
= ± 2√(25/4) / 5
= ± (2 × 5 / 2) / 5
= ± 1

Taking Positive Sign

tan θ = 1
θ = tan⁻¹(1)
θ = 45°

Taking Negative Sign

tan θ = -1
θ = tan⁻¹(-1)
θ = tan⁻¹(tan (180° - 45°))
θ = 135°

Thus, the angle between them is 45° and 135°.
Prove that: tan A + 2tan 2A + 4cot 4A = cot A
✎ Solution
LHS:

tan A + 2tan 2A + 4cot 4A
= tan A + 2tan 2A + 4 / tan 4A
= tan A + 2tan 2A + 4 / tan 2(2A)
= tan A + 2tan 2A + 4 / (2tan 2A / (1 - tan² 2A))
= tan A + 2tan 2A + (2(1 - tan² 2A)) / (tan 2A)
= tan A + (2tan² 2A + 2 - 2tan² 2A) / (tan2A)
= tan A + (1 - tan² A) / tan A
= (tan² A + 1 - tan² A) / tan A)
= 1 / tan A
= cot A
= RHS
Proved.
If A + B + C = π, prove that: sin²A − sin²B + sin²C = 2sinA cosB sinC
✎ Solution:

Here:
A + B + C = π
⇒ A + B = π − C
⇒ sin(A + B) = sin(π − C)
⇒ sin(A + B) = sin C

Now:
LHS = sin²A − sin²B + sin²C
= (1/2)[2sin²A − 2sin²B] + sin²C
= (1/2)[(1 − cos2A) − (1 − cos2B)] + sin²C
= (1/2)[−cos2A + cos2B] + sin²C
= (1/2)[cos2B − cos2A] + sin²C
= (1/2). 2sin[(2A + 2B)/2] sin[(2A − 2B)/2] + sin²C
= sin(A + B) sin(A − B) + sin²C
= sin C sin(A − B) + sin²C
= sinC [sin(A − B) + sinC]
= sinC [sin(A − B) + sin(A + B)]
= sinC . 2sinA cosB
= 2sinA cosB sinC
= RHS
Proved.
From a place at the ground level in front of a tower, the angles of elevation of the top and bottom of a flagstaff 6m high situated at the top of the tower are observed to be 60° and 45°, respectively. Find the height of the tower and the distance between the base of the tower and the point of observation.
✎ Solution:

Let BD be the tower, AD is the flagstaff, and BC is the distance between the base of the tower and the point of observation C.
Given:
AD = 6m
∠BCA = 60° (angle of elevation of the top of the flagstaff)
∠BCD = 45° (angle of elevation of the bottom of the flagstaff)
BD = x (say) Now, in ∆ DCB:
tan 45° = x / BC
⇒ 1 = x / BC
⇒ BC = x
Again, in ∆ACB:
tan 60° = (x + 6) / x
⇒ √3 = (x + 6) / x
⇒ 1.732x = x + 6
⇒ 1.732x − x = 6
⇒ 0.732x = 6
⇒ x = 6 / 0.732
⇒ x = 8.20

Thus, the height of the tower is 8.20 m, and the distance between the base of the tower and the point of observation is 8.20 m.
Find a 2×2 matrix which transforms the unit square

Find the mean deviation from mean and its coefficient from given data:

Marks Obtained	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50
No. of students	2	3	6	5	4

✎ Here,

Marks	No. of students (f)	Mid-value (x)	fx	\|D\| = \|x – x̄\|	f\|D\|
0 – 10	2	5	10	23	46
10 – 20	3	15	45	13	39
20 – 30	6	25	150	3	18
30 – 40	5	35	175	7	35
40 – 50	4	45	180	17	68

N = Σf = 20 Σfx = 560

Now,

∴ Mean = x̄ = Σfx / N = 560 / 20 = 28

∴ Mean Deviation = M.D. = Σf|D| / N = 206 / 20 = 10.3

∴ Coefficient of Mean Deviation = M.D. / x̄ = 10.3 / 28 = 0.37

Find the standard deviation and coefficient of variation from given data:

✎ Here, taking a = 25 and h = 10

Age	No. of persons (f)	Mid-value (x)	d = (x – a) / h	fd	fd²
0 – 10	4	5	-2	-8	16
10 – 20	6	15	-1	-6	6
20 – 30	10	25	0	0	0
30 – 40	20	35	1	20	20
40 – 50	6	45	2	12	24
50 – 60	4	55	3	12	36

N = Σf = 50 Σfd = 30 Σfd² = 102

Now,

Standard Deviation (σ) = h √(Σfd² / N - (Σfd / N)²)

= 10 √(102 / 50 - (30 / 50)²)

= 10 √(2.04 - 0.36)

= 10 √1.68

= 10 × 1.296

= 12.96

Group ‘D’ [4 × 4 = 16]

The sum of three terms in an arithmetic series is 24. If 1, 6, and 18 are added to them respectively, the results are in geometrical series, find the terms.

✎ Let the three consecutive terms in an arithmetic be a – d, a, a + d.

It is given that the sum of these numbers is 24.

a – d + a + a + d = 24

or, 3a = 24

or, a = 24 / 3

∴ a = 8

If 1, 6, and 18 are added to these terms respectively, then a – d + 1, a + 6, a + d + 18 are in geometric series.

Substituting a = 8, we get:

a – d + 1 = 8 – d + 1 = 9 – d

a + 6 = 8 + 6 = 14

a + d + 18 = 8 + d + 18 = 26 + d

i.e., 9 – d, 14, 26 + d are in geometric series.

So, 14² = (9 – d)(26 + d)

or, 196 = 234 + 9d – 26d – d²

or, 196 = 234 – 17d – d²

or, d² + 17d + 196 – 234 = 0

or, d² + 17d – 38 = 0

or, (d + 19)(d – 2) = 0

Either, (d + 19) = 0 ⇒ d = –19

Or, (d – 2) = 0 ⇒ d = 2

When d = –19:

a – d = 8 – (–19) = 27

a = 8

a + d = 8 – 19 = –11

When d = 2:

a – d = 8 – 2 = 6

a = 8

a + d = 8 + 2 = 10

Thus, the required three terms are 27, 8, –11 or 6, 8, 10.
In the given figure, X and Y are the center of circles A and B respectively. Circle A passes through center Y of circle B. If the equation of circle B is x² + y² - 4x + 6y - 12 = 0 and the coordinate of X is (-4, 5), find the equation of circle A.

✎ The equation of circle B is:

x² + y² - 4x + 6y - 12 = 0 ... (i)

Comparing equation (i) with x² + y² + 2gx + 2fy + c = 0, we get

2g = -4, 2f = 6, c = -12

∴ g = -2, f = 3

Center of circle B = Y(-g, -f) = Y(2, -3)

Center of circle A = X(-4, 5) = (h, k)

Now,

Radius of circle A (r) = XY

r = √((x₂ - x₁)² + (y₂ - y₁)²)

r = √((2 + 4)² + (-3 - 5)²)

r = √(36 + 64)

r = √100

r = 10

The equation of circle A is:

(x - h)² + (y - k)² = r²

or, (x + 4)² + (y - 5)² = 10²

or, x² + 2.x.4 + 4² + y² - 2.y.5 + 5² = 100

or, x² + y² + 8x - 10y + 16 + 25 - 100 = 0

∴ x² + y² + 8x - 10y - 59 = 0

By using vector method, prove that the quadrilateral formed by joining the midpoints of adjacent sides of a quadrilateral is a parallelogram.

✎ Given:

ABCD is a quadrilateral. The midpoints of sides AB, BC, CD, DA are P, Q, R, S respectively.

To prove: PQRS is a parallelogram.

Construction: Join A and C.

Proof:

Statements	Reasons
1. PQ = 1/2 AC and PQ // AC	1. In △ABC, the line segment joining the midpoint of two sides of triangle is half of third side and parallel to third side.
2. SR = 1/2 AC and SR // AC	2. In △ADC, the line segment joining the midpoint of two sides of triangle is half of third side and parallel to third side.
3. PQ = SR and PQ // SR	3. From statements (1) and (2).
4. PQRS is a parallelogram	4. From statement (3), being opposite side of quadrilateral equal and parallel.

Proved

The image of the triangle A is A' and image of A' is A'' in the given graph.
1. a) By what transformation the image of the triangle A is A'? Write with reason.
2. b) By what transformation the image of the triangle A' is A''? Write with reason.
3. c) Write the name of transformation which denotes the combined transformation of the above two transformations? Write with reason.
✎ The vertices of triangle A are: (1, 0), (5, 1) and (5, 4).

The vertices of triangle A' are: (-1, 0), (-5, -1) and (-5, -4).

The vertices of triangle A'' are: (0, 1), (1, 5) and (4, 5).

a) When triangle A is transformed into A':
- (1, 0) → (-1, 0)
- (5, 1) → (-5, -1)
- (5, 4) → (-5, -4)
The transformation of triangle A into triangle A' is the rotation through 180° about origin because it follows the rule of the rotation through 180° about origin i.e., (x, y) → (-x, -y).

b) When triangle A' is transformed into A'':
- (-1, 0) → (0, 1)
- (-5, -1) → (1, 5)
- (-5, -4) → (4, 5)
The transformation of triangle A' into triangle A'' is the reflection on y = -x because it follows the rule of the reflection on y = -x i.e., (x, y) → (-y, -x).

c) When triangle A is transformed into A'' (combined transformation):
- (1, 0) → (0, 1)
- (5, 1) → (1, 5)
- (5, 4) → (4, 5)
The combined transformation is the reflection on y = x because it follows the rule of the reflection on y = x i.e., (x, y) → (y, x).

THE END